-
A continuous function at a:

- Greatest integer function: [[x]] is the largest integer that is less than or equal to x. This is one of the most important step functions.
-
Suppose that
 and
and 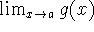 exist. Then
exist. Then
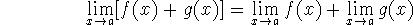
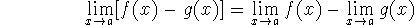
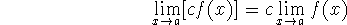
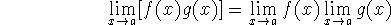
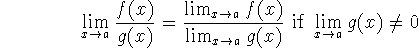
These rules all follow your intuition. For the first one, for example, we could say that ``the limit of the sum is the sum of the limits''.
-
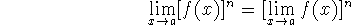
where n is a positive integer (the limit of a power is the power of the limit). ``The limit of the power is the power of the limit.''
-
Two special limits:
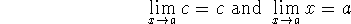
-
Using second special limit and the preceding property,

where n is a positive integer.
-

where n is a positive integer.
-
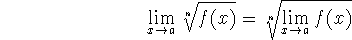
where n is a positive integer.
-
If f is a polynomial or a rational function and a is in the domain of f,
then

For these functions, computing limits is easy!
-
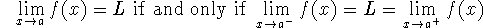
-
If
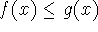 when x is near a (except possibly at a) and the
limits of f and g both exist as x approaches a, then
when x is near a (except possibly at a) and the
limits of f and g both exist as x approaches a, then
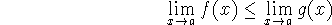
-
Squeeze theorem or Pinching theorem: if
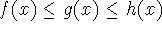 when x is near a (except possibly at a) and
when x is near a (except possibly at a) and
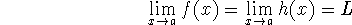
then

The function g is stuck between f and h, and as the functions f and h tend to the same value, g has nowhere to go but the same place!
- All the properties noted above apply to one-sided limits as well.
- Sometimes simplifying an expression (e.g. Example 5, p. 88) or rationalizing an expression (e.g. Example 6, p. 88) makes computation of limits easier.
- There's a nice historical note on Isaac Newton on p. 87.
Many properties of limits are very common sense: sums, differences, products,
quotients, powers, roots, etc. are computed simply. It is especially easy to
compute limits as ![]() for important classes of functions like
polynomials and rational functions: simply evaluate the function at a,
f(a)! The most interesting theorem in this section is probably the pinching
theorem, and the idea of squeezing a function between two others and deducing
properties of the squeezed function from their behavior is very interesting.
for important classes of functions like
polynomials and rational functions: simply evaluate the function at a,
f(a)! The most interesting theorem in this section is probably the pinching
theorem, and the idea of squeezing a function between two others and deducing
properties of the squeezed function from their behavior is very interesting.