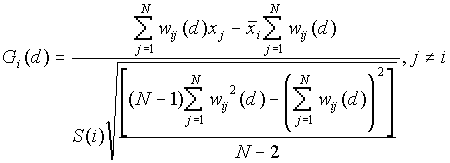Nearest Neighbor Analysis

Local G_i(d) and G_i*(d)

G_i(d) and G_i*(d) are described by Ord and Getis (1995). They indicate the extent to which a location is surrounded by a cluster of high or low values. The G_i(d) statistic excludes the value at i from the summation and is used for spread or diffusion studies, while the G_i*(d) includes the value at i in the summation and is most often used for studies of clustering.

Input

You’ll be asked to enter the input data file. This file should contain N rows coordinates, and the corresponding value of the test variable (x).

Analysis

The null hypothesis in both of these tests is that there is no association between the value found at one site and its neighbors within the specified distance. The expected value under the null hypothesis is 0, and the variance is 1. Therefore, the G_i(d) or G_i*(d ) statistics may be examined as a standard normal variate. Positive G_i(d) or G_i*(d) indicate spatial association of high values, whereas negative G_i(d) or G_i*(d) indicate spatial association of low values.

Formula

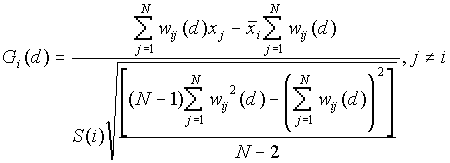[1]

where

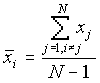
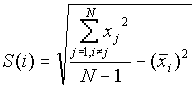
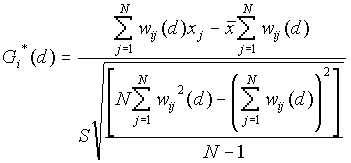[2]

where

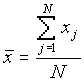
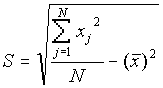
Output

The output file includes the total number of points in the analysis, and a listing of the G_i(d) or G_i*(d) value for each point at each distance specified.

Example G_i*(d)

For this example we will examine the clustering of high versus low cancer rates in New Mexico’s counties using the G_i*(d) statistic. The data are taken from the National Cancer Institute Biometry Research Group Datasets, and it is available on their website (http://dcp.nci.nih.gov/bb/datasets.html). The total number of cases diagnosed between 1980 and 1989 were divided by the 1985 population estimate to determine the cancer rate (cases per 10,000 population) of each county. These data are shown in Table 1. The points used for this analysis are the county seats, and the coordinate units are kilometers. Figure 1 is a map of these county seats

Table 1: Cancer Rates of New Mexico Counties

ID Number	County	Coordinates		Cancer Rate
1	Bernalillo	219	338	40.29
2	Catron	027	189	33.12
3	Chaves	418	156	76.91
4	Colfax	408	538	47.37
5	Curry	534	262	35.19
6	DeBaca	438	272	73.98
7	DonaAna	212	037	36.67
8	Eddy	451	037	68.35
9	Grant	073	083	37.90
10	Guadelupe	428	322	31.24
11	Harding	458	418	27.23
12	Hidalgo	033	040	44.43
13	Lea	528	103	41.38
14	Lincoln	295	179	63.39
15	Los Alamos	246	425	25.56
16	Luna	119	030	80.02
17	McKinley	030	385	11.78
18	Mora	335	435	42.69
19	Otero	289	100	32.19
20	Quay	481	345	68.23
21	Rio Arriba	222	514	24.21
22	Roosevelt	518	239	38.90
23	Sandoval	229	365	48.29
24	San Juan	096	531	27.30
25	San Miguel	345	398	31.54
26	SantaFe	279	402	34.77
27	Sierra	166	127	140.73
28	Socorro	199	222	37.79
29	Taos	315	484	26.60
30	Torrance	272	302	66.59
31	Union	521	488	52.70
32	Valencia	160	329	45.19

Figure 1: New Mexico County Seats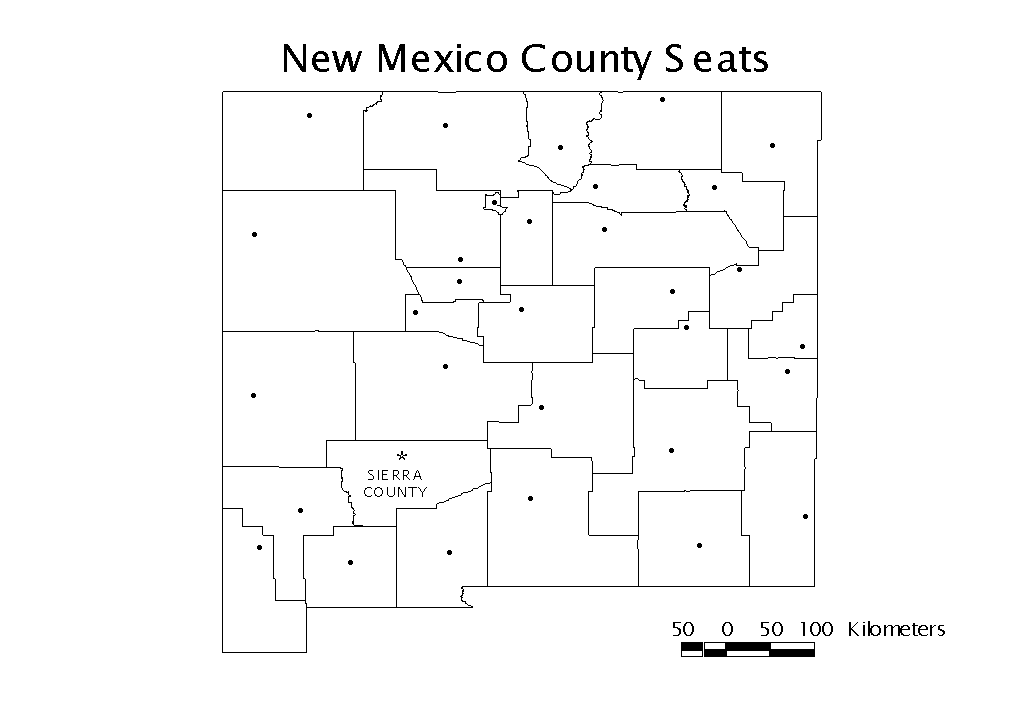

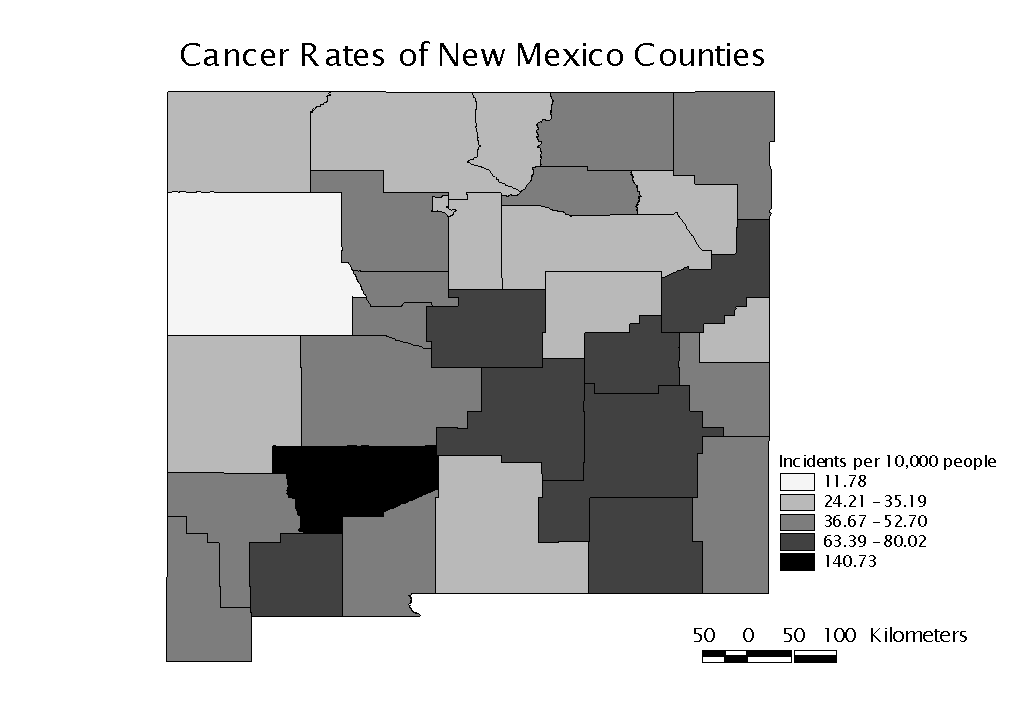
Sierra County, with a rate of 140.73 per 10,000 population, has a much higher rate than all other counties. The next highest cancer rate is 80.02 cases per 10,000 people in Luna County. We will examine the county data using the G* statistic to determine if this disparity stands alone or is the center of a cluster. Figure 2 is a map of the distribution of cancer rates by county.

Figure 2: Cancer rates of New Mexico Counties

A summary table of the G_i*(d) values for Sierra County is shown in Table 2. Recall that the G_i*(d) statistic is based on accumulated clustering tendencies. The complete output file is included in Table 3.

Table 2: G_i* values for Sierra County (observation #27)

Distance(d)	50km	100km	150km	200km	250km	300km
G_i*(d)	3.95	3.95	1.81	1.40	1.49	1.54

Clustering is in evidence at 50km and 100km, but as distance increases the tendancy for clustering decreases. Since the next closest point to the Sierra County Seat is over 100km away, this indicates that Sierra County stands alone as a cluster. As the neighboring counties are considered the G_i*(d) values drop, and this implies that anti-clustering forces are in command.

Table 3: Output File

The input data file: nmlung.txt The total number of points: 32 Distance: 50.000000 # Gi*(d) 1 -0.14201 2 -0.56799 3 1.27146 4 0.03060 5 -0.57951 6 1.14838 7 -0.41887 8 0.91189 9 -0.36720 10 -0.64696 11 -0.81540 12 -0.09290 13 -0.22102 14 0.70354 15 -0.99498 16 1.40210 17 -1.46440 18 -0.57529 19 -0.60705 20 0.90685 21 -0.94226 22 -0.57951 23 -0.14201 24 -0.81246 25 -0.57529 26 -0.99498 27 3.95229 28 -0.37182 29 -0.84187 30 0.83796 31 0.25449 32 -0.06097 Distance: 100.000000 # Gi*(d) 1 -0.35877 2 -0.56799 3 1.27146 4 0.03060 5 0.65710 6 0.28850 7 0.22455 8 0.91189 9 0.56230 10 0.84063 11 0.20650 12 0.56230 13 -0.22102 14 0.06935 15 -1.48652 16 0.27522 17 -1.46440 18 -1.45026 19 -0.19244 20 0.05359 21 -1.59361 22 0.20424 23 -0.35877 24 -0.81246 25 -1.12633 26 -1.35693 27 3.95229 28 -0.37182 29 -1.76916 30 0.38227 31 -0.40318 32 -0.15433 Distance: 150.000000 # Gi*(d) 1 -0.72769 2 -0.61369 3 1.21299 4 -0.73709 5 0.28850 6 0.44533 7 1.89823 8 1.17137 9 1.74185 10 -0.40733 11 0.03118 12 0.19677 13 0.86130 14 2.57943 15 -1.27227 16 2.14461 17 -1.09643 18 -1.64603 19 2.34872 20 -0.23837 21 -1.71618 22 0.69550 23 -1.37782 24 -1.26129 25 -1.07759 26 -1.27227 27 1.80685 28 2.04694 29 -1.55458 30 -0.47802 31 0.19809 32 -1.06122 Distance: 200.000000 # Gi*(d) 1 -1.60199 2 0.97606 3 0.99883 4 -1.74106 5 0.33635 6 0.56721 7 1.68767 8 0.71302 9 1.48808 10 0.25014 11 -0.74365 12 1.74185 13 1.02729 14 2.07760 15 -1.49910 16 1.38907 17 -1.52031 18 -0.85436 19 2.74986 20 0.19228 21 -1.83500 22 0.33635 23 -1.09888 24 -2.15949 25 -0.87391 26 -1.82133 27 1.40557 28 0.86386 29 -1.71076 30 -0.57175 31 -0.45067 32 -1.75313 Distance: 250.000000 # Gi*(d) 1 -0.72829 2 0.65445 3 0.95940 4 -1.49865 5 0.50154 6 -0.24102 7 2.13038 8 0.76704 9 1.40557 10 -0.33502 11 -0.71390 12 1.48808 13 0.99883 14 2.43843 15 -1.89907 16 1.40557 17 -2.17783 18 -0.87391 19 2.82523 20 -0.12649 21 -1.99650 22 0.74490 23 -0.59005 24 -2.20728 25 -1.07311 26 -1.66895 27 1.49201 28 0.89900 29 -1.15890 30 0.76238 31 -0.57532 32 -0.67862 Distance: 300.000000 # Gi*(d) 1 -0.41366 2 0.96351 3 1.56281 4 -0.85436 5 0.57030 6 -0.26637 7 2.33549 8 1.93695 9 1.48872 10 -0.65520 11 -0.45403 12 1.40557 13 0.99883 14 1.68321 15 -1.60165 16 1.40557 17 -0.36352 18 -0.94853 19 2.10932 20 -0.19851 21 -2.59936 22 0.57030 23 -0.25629 24 -2.03640 25 -0.94853 26 -0.01566 27 1.54522 28 0.21334 29 -1.29619 30 -1.08038 31 -1.04677 32 -1.04106

References

Ord, J.K. and Getis, A., (1995) Local Spatial Autocorrelation Statistics: Distribution Issues and an Application, Geographical Analysis, 27(4): 286-306

National Cancer Institute Biometry Research Group Datasets http://dcp.nci.nih.gov/bb/datasets.html