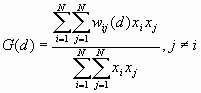
The General G(d) Statistic

The General G(d) statistic is a multiplicative measure of overall spatial association of values which fall within a given distance of each other. It was developed by Getis and Ord (1992).

1. The input data file should contain the X,Y coordinates and the value at each point.
2. The maximum distance of study.
3. The number of distance increments within the maximum distance of study.
4. The output file name.

A G(d) value higher than the expected G(d) indicates a clustering of high values, and a G(d) lower than the expected G(d) indicates a clustering of low values. The variance of G(d) and a Z-value (standard variates) are calculated to determine the level of significance.

For a chosen critical distance d, G(d) is

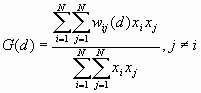
where is the value of the ith point and

is the weight for point i and j for distance d.

The expected mean value of G(d) is

The variance of G(d) is

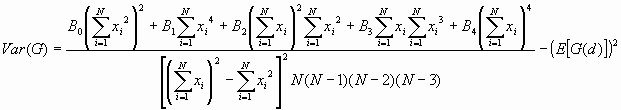
where

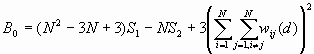
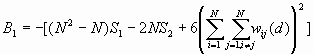
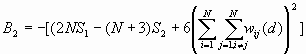
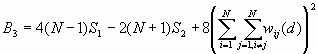
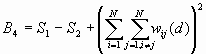
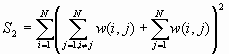
The Z-value is calculated as:

1. The number of points
2. G(d), Expected G(d), Var(G), and Z-value for each specified distance

For this example we will consider the distribution of AIDS rates for the counties of California. The data are taken from the Department of Health Services of the State of California (1999). The rates are cumulative incidences since 1981 per 100,000 population. The data are shown in Table 1. A map showing the AIDS rates by county is shown in Figure 1.

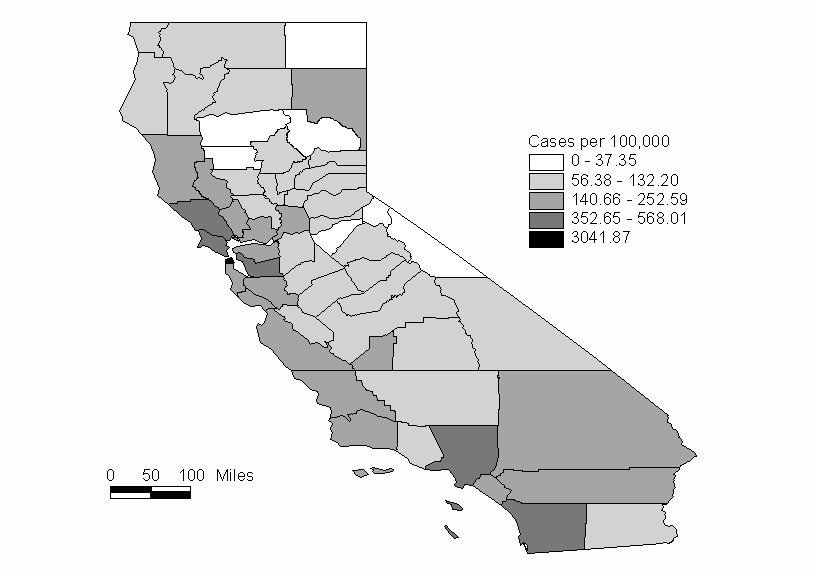
The G(d) statistic is computed for 50 mile increments from 50 to 250 miles. The output file is shown as Table 2. The highest Z-value (4.93) is found at a distance of 50 miles, and the Z-values decrease as the distance is increased. The Z value from the tables of the normal distribution for a =0.05 (2-tail) is +/-1.96. At the a =0.05 level, there is significant clustering of high AIDS rates for distances of 50 and 100 miles. This clustering is most evident in the San Fransisco Bay area (Figure 1). As the distance of study is increased, the clustering tendancies of high AIDS rates decrease.

Table 2: Output

The input data file: aids.dat
The total number of points:  58
   Distance      G(d)    Expected G(d)  Variance      Z-value
    50.0000    0.19054      0.0587       0.00071       4.9314
   100.0000    0.35785      0.2202       0.00483       1.9814
   150.0000    0.49061      0.3975       0.00983       0.9393
   200.0000    0.57358      0.5299       0.01149       0.4070
   250.0000    0.64102      0.6231       0.01116       0.1696

Getis, A. and Ord, J.K. (1992) The Analysis of Spatial Assosciation by Use of Distance Statistics, Geographical Analysis, 24: 189-206.

Getis, A., and Ord, J.K. (1998), "Spatial Modelling of Disease Dispersion Using a Local Statistic: The Case of AIDS," Chapter 12 in D.A. Griffith, C.G Amrhein, and J-M Huriot (eds.) Econometric Advances in Spatial Modelling and Methodology: Essays in Honour of Jean Paelinck, Kluwer.

State of California Department of Health Services (1999). 1998 Report Health Data Summaries for California Counties.