Local Moran’s I

Local Moran’s I is a local spatial autocorrelation statistic based on the Moran’s I statistic. It was developed by Anselin(1995) as a local indicator of spatial association or LISA statistic. Anselin defines LISA statistics as having the following two properties:

  1. "The LISA for each observation gives an indication of the extent of significant spatial clustering of similar values around that observation"; and
  2. "the sum of LISAs for all observations is proportional to a global indicator of spatial association."
See Anselin(1995) for a complete discussion of Local Moran’s I and LISAs.

Input
  1. Input data file, which includes X,Y coordinates and the values at each point.
  2. The maximum study distance (d).
  3. The number of bands within d.
  4. The weights matrix file name or the parameter m used to weight the influence of distance (see below).
  5. Output file name.

Analysis

Analysis is very similar to that of global Moran’s I. Values of Ii that exceed E[Ii] indicate positive spatial autocorrelation, in which similar values, either high values or low values are spatially clustered around point i. Values of Ii below E[Ii] indicate negative spatial autocorrelation, in which neighboring values are dissimilar to the value at point i. Again, a normally distributed Z statistic (2-tailed) is calculated to determine significance.

There are two types of spatial weighting methods that may be used (#4 above, under input):

  1. The input can be a spatial weights matrix file which allows the researcher to introduce his/her own notion of spatial structure, e.g. a contiguity matrix where touching regions are given a value of 1 and all others are set to 0.
  2. The input can also be a weight, m, that the distance is raised in order to show the influence of distance. An example of this might be , in which d is raised to the power of m=2. For this type of weighting scheme, the statistic is calculated for bands only.
Bear in mind that each Ii value for a given site i represents association between the ith site and only the j values in a given band (see Figure 1).

 

Figure1: Analysis by Bands

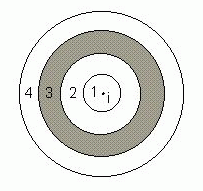
In this example, Ii gives the statistic’s value for the association between i and all j points in band 3.

Formula

Where

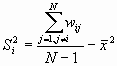
And

Remember, when this weighting scheme is used, the statistic is calculated for bands only. A spatial weights matrix may also be used.

For a randomization hypothesis, the expected value is

 

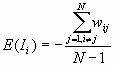
The variance is

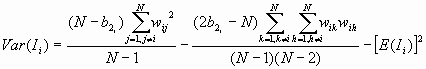
Where

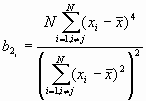
Output

The output file includes the input data file and the total number of points. For each specified distance the following table is printed.

Observation #

Observed Ii

Expected Ii

Variance

Z-value

1

2

⋮

        

Example

For this example we will consider the same data that are used for the Moran’s I and Geary’s c example. Recall that we are examining the distribution of hepatitis rates for the counties of California. A complete listing of the data is included in the Moran’s I and Geary’s c example. A map of California showing the Hepatitis rates is shown in Figure 2.

 

Figure 2: Hepatitis Rates of California Counties in 1998 (per 100,000 pop.)

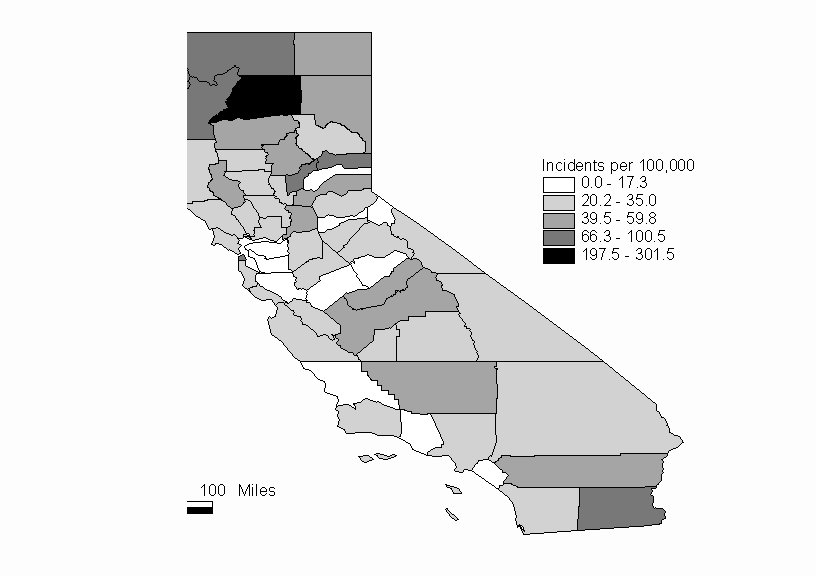
In this analysis, using Local Moran’s I, we will look for spatial association around each individual location. We will use a contiguity matrix as our spatial weighting scheme. The statistically significant Ii are shown in Table 1, and Table 2 is the complete listing of Ii values.

Table 1: Ii results for selected counties

County

Observation #

Ii

E[Ii]

Variance

Z-value

Del Norte

8

44.4954

-0.0351

1.2844

39.2923

Shasta

45

11.5026

-0.1053

3.7221

6.0167

Humboldt

12

9.1911

-0.0702

2.5251

5.8282

Siskyou

47

8.5660

-0.0877

3.1290

4.8921

Trinity

53

3.9381

-0.0877

3.1290

2.2759

It appears from the map that there is a grouping of high hepatitis rates in the northwest corner of California. The Local Moran’s I analysis can be used to confirm that there is positive spatial autocorrelation in this area. In fact, we find that the five counties with significant Ii are located in this part of the state. We can conclude from this analysis using Local Moran’s I that there is a clustering of high hepatitis rates, and that it includes these five counties.

 

Table 2: Output File

 
The input data file: hep.dat
The total number of points:  58
The weight matrix file is ca.mat
     #   Moran's Ii  Expected I  Variance   Z-value
     1     0.8837    -0.1053     3.7221     0.5126
     2     1.8892    -0.0877     3.1290     1.1176
     3     1.2223    -0.0877     3.1290     0.7406
     4     0.0411    -0.1053     3.7221     0.0758
     5     1.1651    -0.0877     3.1290     0.7082
     6     0.2009    -0.0877     3.1290     0.1632
     7     0.3317    -0.0877     3.1290     0.2371
     8    44.4954    -0.0351     1.2844    39.2923
     9     0.3256    -0.0702     2.5251     0.2491
    10    -0.6235    -0.1404     4.8753    -0.2188
    11     0.0405    -0.0877     3.1290     0.0725
    12     9.1911    -0.0702     2.5251     5.8282
    13    -0.1891    -0.0351     1.2844    -0.1359
    14     0.1420    -0.0877     3.1290     0.1298
    15     0.1043    -0.1404     4.8753     0.1108
    16     0.4835    -0.0877     3.1290     0.3229
    17     0.1352    -0.1053     3.7221     0.1246
    18     1.6039    -0.0702     2.5251     1.0535
    19     0.6348    -0.0702     2.5251     0.4437
    20    -0.0906    -0.0877     3.1290    -0.0016
    21    -0.1857    -0.0351     1.2844    -0.1329
    22     0.9326    -0.0702     2.5251     0.6311
    23    -0.5525    -0.1053     3.7221    -0.2318
    24     0.9810    -0.1053     3.7221     0.5631
    25     1.7040    -0.0526     1.9102     1.2710
    26     0.3364    -0.0877     3.1290     0.2398
    27     0.5522    -0.0877     3.1290     0.3618
    28     0.4651    -0.0702     2.5251     0.3368
    29    -1.1022    -0.0526     1.9102    -0.7594
    30     0.5609    -0.0702     2.5251     0.3971
    31    -0.0466    -0.0877     3.1290     0.0233
    32    -1.0320    -0.1053     3.7221    -0.4804
    33    -0.0571    -0.0702     2.5251     0.0082
    34    -0.0260    -0.1404     4.8753     0.0518
    35     0.6128    -0.0877     3.1290     0.3960
    36     0.1537    -0.0702     2.5251     0.1409
    37     0.1858    -0.0702     2.5251     0.1611
    38    -1.7069    -0.0702     2.5251    -1.0300
    39     0.8753    -0.1228     4.3042     0.4811
    40     0.8197    -0.0702     2.5251     0.5600
    41     0.2681    -0.0702     2.5251     0.2129
    42     0.5061    -0.0526     1.9102     0.4043
    43     1.7154    -0.1228     4.3042     0.8860
    44     0.5447    -0.0702     2.5251     0.3869
    45    11.5026    -0.1053     3.7221     6.0167
    46     0.2991    -0.0702     2.5251     0.2324
    47     8.5660    -0.0877     3.1290     4.8921
    48     0.7069    -0.0877     3.1290     0.4492
    49     0.6700    -0.0877     3.1290     0.4284
    50     0.6463    -0.1228     4.3042     0.3707
    51    -0.1200    -0.1053     3.7221    -0.0077
    52     1.2646    -0.1053     3.7221     0.7100
    53     3.9381    -0.0877     3.1290     2.2759
    54     0.1417    -0.0702     2.5251     0.1333
    55     1.2367    -0.1053     3.7221     0.6956
    56     0.5148    -0.0526     1.9102     0.4106
    57     0.3960    -0.1053     3.7221     0.2598
    58     0.1348    -0.1053     3.7221     0.1244

References

Anselin, L. (1995) "The Local Indicators of Spatial Association – LISA", Geographical Analysis, 27: 93-115.

State of California Department of Health Services (1999). 1998 Report Health Data Summaries for California Counties.